一. 绘制路径(path)基本知识

图形的基本元素是路径。

路径是通过不同颜色和宽度的线段或曲线相连形成的不同形状的点的集合。

一个路径，甚至一个子路径，都是闭合的。

使用路径绘制图形需要一些额外的步骤：

1. 创建路径起始点
2. 调用绘制方法去绘制出路径
3. 把路径封闭
4. 一旦路径生成，通过描边或填充路径区域来渲染图形。

下面是需要用到的方法：

1. beginPath()

   新建一条路径，路径一旦创建成功，图形绘制命令被指向到路径上生成路径

2. moveTo(x, y)

   把画笔移动到指定的坐标(x, y)。相当于设置路径的起始点坐标。

3. closePath()

   闭合路径之后，图形绘制命令又重新指向到上下文中

4. stroke()

   通过线条来绘制图形轮廓

5. fill()

   通过填充路径的内容区域生成实心的图形

二. 绘制线段

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath(); //新建一条path
    ctx.moveTo(50, 50); //把画笔移动到指定的坐标
    ctx.lineTo(200, 50);  //绘制一条从当前位置到指定坐标(200, 50)的直线.
    //闭合路径。会拉一条从当前点到path起始点的直线。如果当前点与起始点重合，则什么都不做
    ctx.closePath();
    ctx.stroke(); //绘制路径。
}
draw();

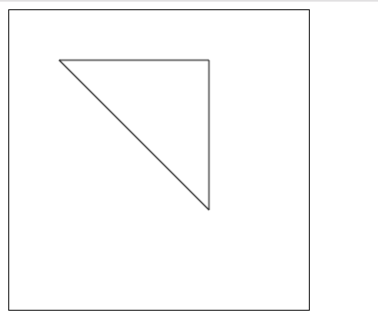
二. 绘制三角形边框

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath();
    ctx.moveTo(50, 50);
    ctx.lineTo(200, 50);
    ctx.lineTo(200, 200);
      ctx.closePath(); //虽然我们只绘制了两条线段，但是closePath会closePath，仍然是一个3角形
    ctx.stroke(); //描边。stroke不会自动closePath()
}
draw();

四. 填充三角形

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath();
    ctx.moveTo(50, 50);
    ctx.lineTo(200, 50);
    ctx.lineTo(200, 200);

    ctx.fill(); //填充闭合区域。如果path没有闭合，则fill()会自动闭合路径。
}
draw();

五. 绘制圆弧

有两个方法可以绘制圆弧：

1. arc(x, y, r, startAngle, endAngle, anticlockwise):

   以(x, y)为圆心，以r为半径，从 startAngle弧度开始到endAngle弧度结束。anticlosewise是布尔值，true表示逆时针，false表示顺时针。(默认是顺时针)

   注意：

   1. 这里的度数都是弧度。
   2. 0弧度是指的x轴正方形

   radians=(Math.PI/180)*degrees   //角度转换成弧度
   

2. arcTo(x1, y1, x2, y2, radius):

   根据给定的控制点和半径画一段圆弧，最后再以直线连接两个控制点。

圆弧案例1：

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath();
    ctx.arc(50, 50, 40, 0, Math.PI / 2, false);
    ctx.stroke();
}
draw();

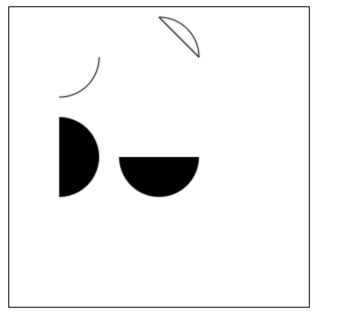
圆弧案例2：

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath();
    ctx.arc(50, 50, 40, 0, Math.PI / 2, false);
    ctx.stroke();

    ctx.beginPath();
    ctx.arc(150, 50, 40, 0, -Math.PI / 2, true);
    ctx.closePath();
    ctx.stroke();

    ctx.beginPath();
    ctx.arc(50, 150, 40, -Math.PI / 2, Math.PI / 2, false);
    ctx.fill();

    ctx.beginPath();
    ctx.arc(150, 150, 40, 0, Math.PI, false);
    ctx.fill();

}
draw();

圆弧案例3：

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath();
    ctx.moveTo(50, 50);
      //参数1、2：控制点1坐标   参数3、4：控制点2坐标  参数4：圆弧半径
    ctx.arcTo(200, 50, 200, 200, 100);
    ctx.lineTo(200, 200)
    ctx.stroke();

    ctx.beginPath();
    ctx.rect(50, 50, 10, 10);
    ctx.rect(200, 50, 10, 10)
    ctx.rect(200, 200, 10, 10)
    ctx.fill()
}
draw();

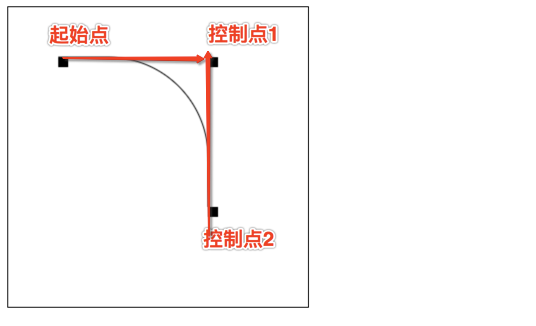
arcTo方法的说明：

​ 这个方法可以这样理解。绘制的弧形是由两条切线所决定。

​ 第 1 条切线：起始点和控制点1决定的直线。

​ 第 2 条切线：控制点1 和控制点2决定的直线。

​ 其实绘制的圆弧就是与这两条直线相切的圆弧。

六. 绘制贝塞尔曲线

什么是贝塞尔曲线

​ 贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。

​ 一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。

​ 贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具如PhotoShop等。在Flash4中还没有完整的曲线工具，而在Flash5里面已经提供出贝塞尔曲线工具。

​ 贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。

一次贝塞尔曲线(线性贝塞尔曲线)

​ 一次贝塞尔曲线其实是一条直线。

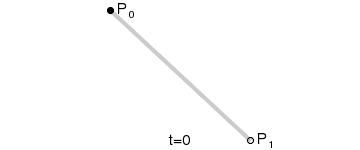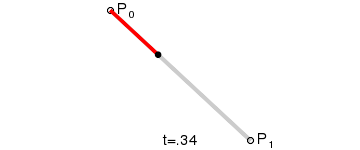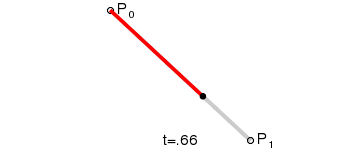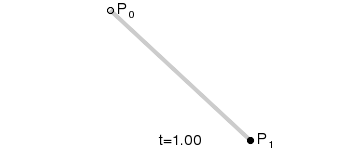
二次贝塞尔曲线

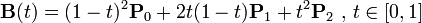
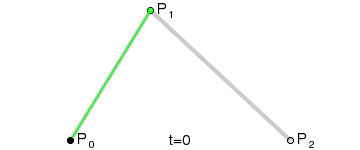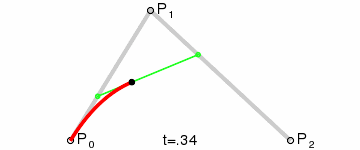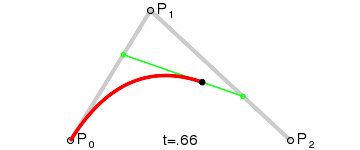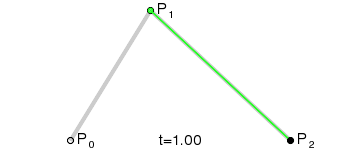
选定一个0-1的t值
通过P0和P1计算出点Q0，Q0在P0 P1连成的直线上，并且length( P0, Q0 ) = length( P0, P1 ) * t

同样，通过P1和P2计算出Q1，使得length( P1, Q1 ) = length( P1, P2 ) * t
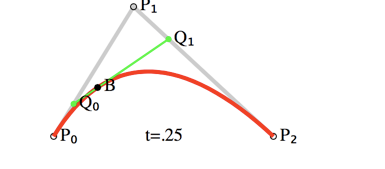
再重复一次这个步骤，通过Q1和Q2计算出B，使得length( Q0, Q1 ) = length( Q0, B ) * t。

B就为当前曲线上的点

注：上面的length表示两点之间的长度

三次贝塞尔曲线

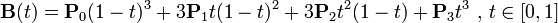
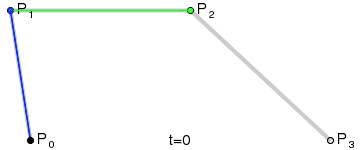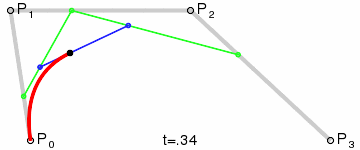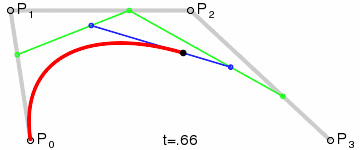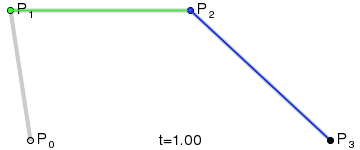
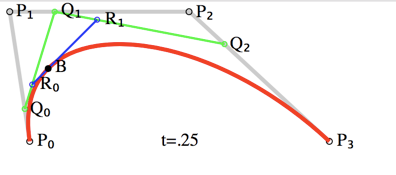
绘制贝塞尔曲线

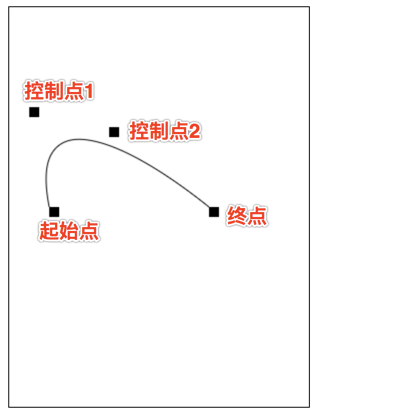
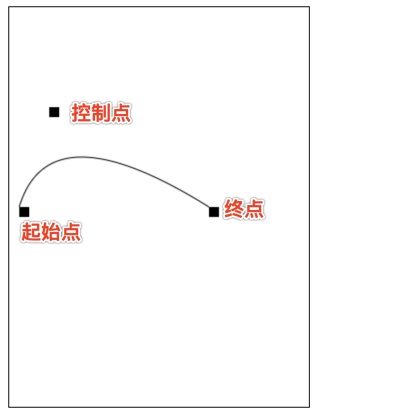
绘制二次贝塞尔曲线

quadraticCurveTo(cp1x, cp1y, x, y):

说明：

​ 参数1和2：控制点坐标

​ 参数3和4：结束点坐标

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath();
    ctx.moveTo(10, 200); //起始点
    var cp1x = 40, cp1y = 100;  //控制点
    var x = 200, y = 200; // 结束点
    //绘制二次贝塞尔曲线
    ctx.quadraticCurveTo(cp1x, cp1y, x, y);
    ctx.stroke();

    ctx.beginPath();
    ctx.rect(10, 200, 10, 10);
    ctx.rect(cp1x, cp1y, 10, 10);
    ctx.rect(x, y, 10, 10);
    ctx.fill();

}
draw();

绘制三次贝塞尔曲线

bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)：

说明：

​ 参数1和2：控制点1的坐标

​ 参数3和4：控制点2的坐标

​ 参数5和6：结束点的坐标

function draw(){
    var canvas = document.getElementById('tutorial');
    if (!canvas.getContext) return;
    var ctx = canvas.getContext("2d");
    ctx.beginPath();
    ctx.moveTo(40, 200); //起始点
    var cp1x = 20, cp1y = 100;  //控制点1
    var cp2x = 100, cp2y = 120;  //控制点2
    var x = 200, y = 200; // 结束点
    //绘制二次贝塞尔曲线
    ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y);
    ctx.stroke();

    ctx.beginPath();
    ctx.rect(40, 200, 10, 10);
    ctx.rect(cp1x, cp1y, 10, 10);
    ctx.rect(cp2x, cp2y, 10, 10);
    ctx.rect(x, y, 10, 10);
    ctx.fill();

}
draw();